计数排序和基数排序是一种非基于比较的排序算法。它在处理一定范围内的整数排序时,快于任何比较排序算法。但是,这是一种牺牲空间换取时间的做法。
计数排序
基本思想
对每一个输入元素x,确定出小于x的元素个数。这样,我们就可以直接把x放到它在输出数组中的位置上了。
这个算法需要一个额外的数组来记录计数,所以如果范围非常大的话,可能需要较大的空间。
算法思想

其实会发现一个主要问题,那么就是tmp数组到底应该开辟多大的空间,怎么计算?
假设我们有组数据:100, 101, 102, 101, 109, 105, 105
我们应该开辟多大的空间,因为最大值是109,从0开始需要开辟110个空间吗?那太浪费了。

所以我们只需要 最大值 — 最小值 + 1 的空间,max=109, min=100, max-min+1=10 ,即可
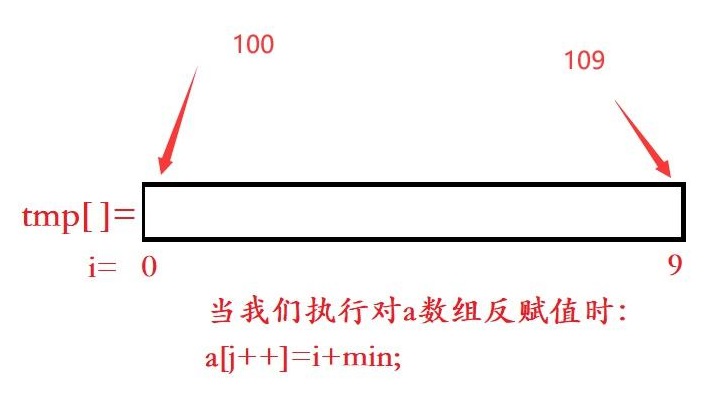
代码流程图

java
public static void countSort(int[] a) {
// 初始化数组中的最大值和最小值
int max = a[0];
int min = a[0];
// 遍历数组,找到最大值和最小值
for (int i = 0; i < a.length; i++) {
if (a[i] > max) {
max = a[i];
}
if (a[i] < min) {
min = a[i];
}
}
// 计算整数范围,为count数组的大小
int range = max + 1 - min;
// 初始化计数数组
int[] count = new int[range];
// 遍历原数组,计算每个数出现的次数并保存到count数组中
for (int i = 0; i < a.length; i++) {
count[a[i] - min]++;
}
// 对count数组进行累加
for (int i = 1; i < range; i++) {
count[i] += count[i - 1];
}
// 初始化一个与原数组等规模的辅助数组
int[] tmp = new int[a.length];
// 从原数组最后一个元素开始,将每个元素放到临时数组中对应的位置,并更新count数组
for (int i = a.length - 1; i >= 0; i--) {
tmp[count[a[i] - min] - 1] = a[i];
count[a[i] - min]--;
}
// 将临时数组的元素复制回原数组,完成排序
for (int i = 0; i < a.length; i++) {
a[i] = tmp[i];
}
}
基数排序
计数排序和基数排序都可以看作是桶排序。计数排序是特殊的桶排序,当桶的个数取最大 max-min+1 的时候,就变成了计数排序。而基数排序则是按数位来划分桶(如:十进制就对应10个桶),每个数位上都进行一轮桶排序,因此可以看做是多轮桶排序。
Java
public static void main(String[] args) {
int[] arr = {10, 2, 3, 5, 1, 15, 4, 20, 7, 30};
radixSort(arr);
System.out.println(Arrays.toString(arr));
}
public static void radixSort(int[] arr) {
// 检查输入的数组是否为空或者只有一个元素
if (arr == null || arr.length < 2) return;
radixSort(arr, 0, arr.length - 1, maxbits(arr));
}
// 计算数组中的最大数的
public static int maxbits(int[] arr) {
// 首先将数组中的所有元素进行比较,找出最大值,然后通过不断地将最大值除以10并向下取整,直到最大值不再变化,这样就得到了最大值的位数
int max = Integer.MIN_VALUE;
for (int i = 0; i < arr.length; i++) {
max = Math.max(max, arr[i]);
}
int res = 0;
while (max != 0) {
res++;
max /= 10;
}
return res;
}
// 基数排序的主要部分,用于对数组arr的子数组(由L和R定义)进行排序
public static void radixSort(int[] arr, int L, int R, int digit) {
final int radix = 10; // 基数(即数字系统的基数量)为10
int i = 0, j = 0;
// 创建一个用于存放排序结果的桶数组,大小为子数组的长度
int[] bucket = new int[R - L + 1];
// 对于每个位数(从最低位到最高位)进行排序
for (int d = 1; d <= digit; d++) {
// 10个空间
// count[0] 当前为(d位)是0的数字有多少个
// count[1] 当前为(d位)是(0和1)的数字有多少个
// count[2] 当前为(d位)是(0、1和2)的数字有多少个
// count[i] 当前为(d位)是(0~i)的数字有多少个
int[] count = new int[radix]; // 创建一个计数数组,用于记录每个数字在该位上的数量
// 遍历子数组
for (i = L; i <= R; i++) {
// 获取当前元素在第d位上的值
j = getDigit(arr[i], d);
// 增加对应位置的计数
count[j]++;
}
// 将计数数组进行累加,为桶排序做准备
for (i = 1; i < radix; i++) {
count[i] = count[i] + count[i - 1];
}
// 从后往前遍历子数组,将元素放入对应的桶中
for (i = R; i >= L; i--) {
j = getDigit(arr[i], d);
bucket[count[j] - 1] = arr[i];
count[j]--;
}
// 将桶中的元素按顺序放回原数组
for (i = L, j = 0; i <= R; i++, j++) {
arr[i] = bucket[j];
}
}
}
// 用于获取一个整数x的第d位上的数字
public static int getDigit(int x, int d){
// 通过除以10的d-1次方再取余数,获取x的第d位上的数字
return ((x / ((int) Math.pow(10, d - 1))) % 10);
}
文档信息
- 本文作者:carpe
- 本文链接:https://carpedx.com/wiki/algorithm-count-sort/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)