快速排序,又称分区交换排序,简称快排,是一种被广泛运用的排序算法
堆排序是一种基于大根堆或小根堆的排序算法,利用堆这种数据结构所设计的一种排序算法。堆排序是一种选择排序,它的最坏,最好,平均时间复杂度均为O(nlogn),它也是不稳定排序。
堆结构
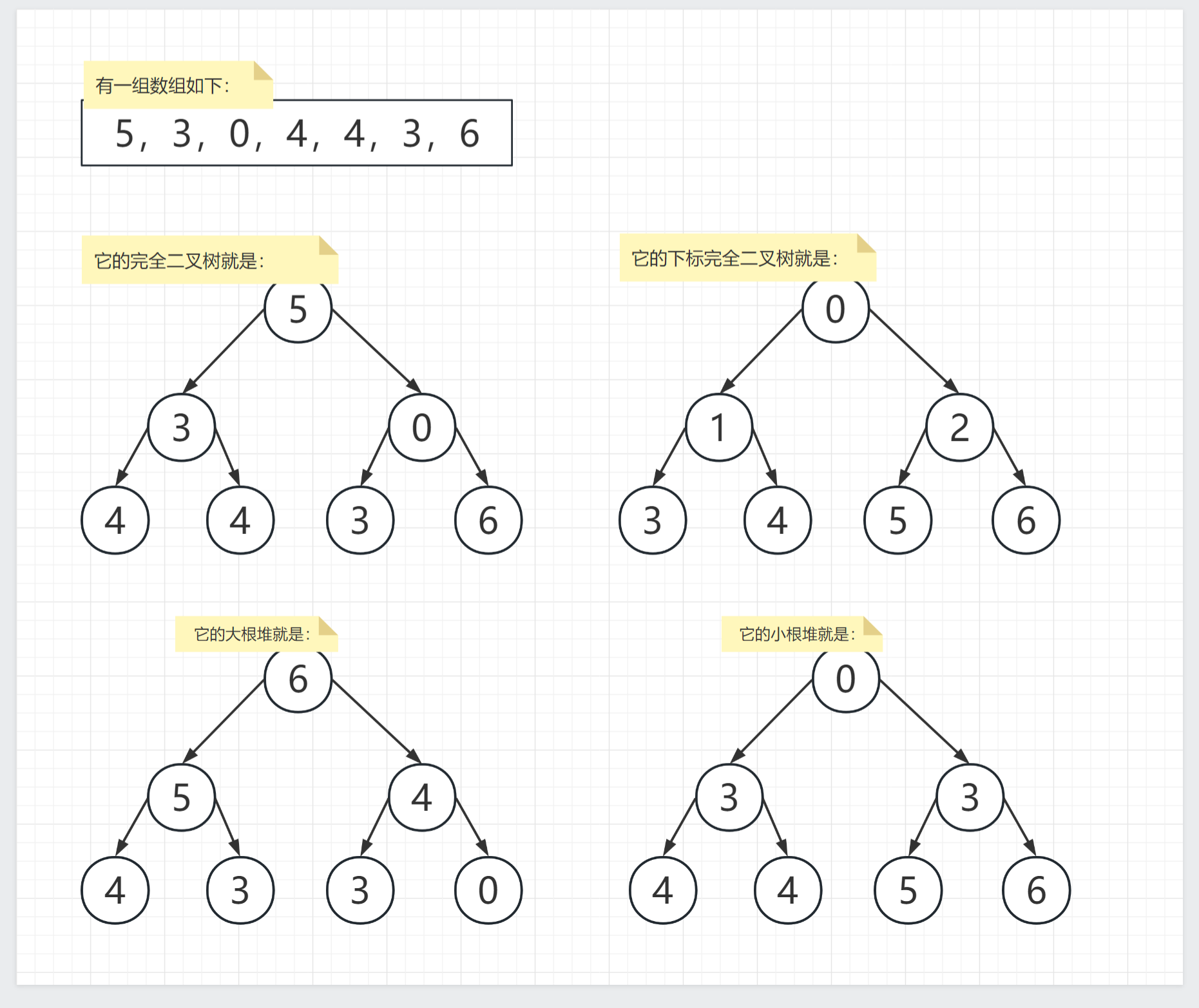
流程图
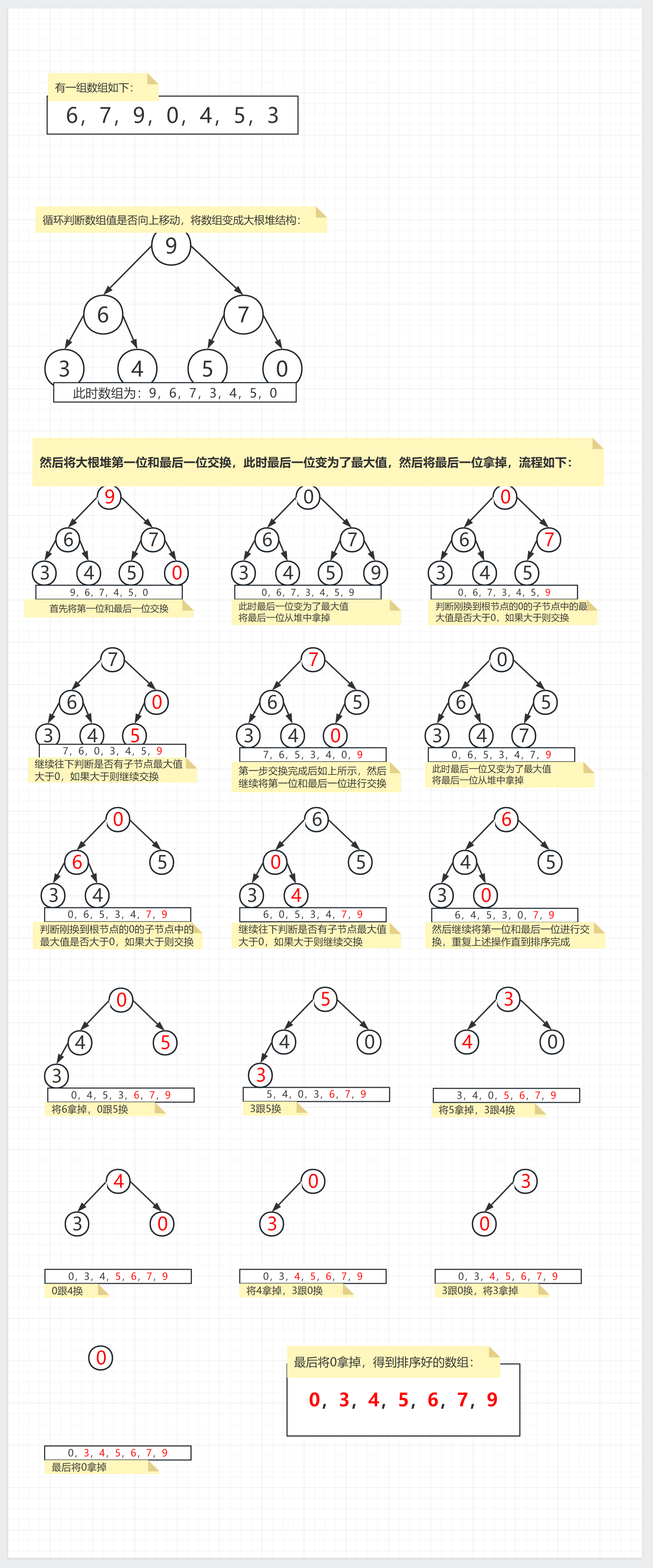
java
public static void main(String[] args) {
int[] arr = {6, 7, 9, 0, 4, 5, 3};
heapSort(arr);
System.out.println(Arrays.toString(arr));
}
// 堆排序
public static void heapSort(int[] arr) {
if (arr == null || arr.length < 2) return;
// 将当前元素放入大根堆中
// 方式一:判断能否往上移动
for (int i = 0; i < arr.length; i++) {
heapInsert(arr, i);
}
// 方式二:判断能否往下移动
/* for (int i = arr.length - 1; i >= 0; i--) {
heapIfy(arr, i);
} */
// 定义堆数组长度
int heapSize = arr.length;
// 将堆顶元素(即数组的第一个元素)和最后一个元素交换,同时减小heapSize
swap(arr, 0, --heapSize);
// 如果堆数组不止剩最后一个元素
while (heapSize > 0) {
// 刚交换到堆顶的元素判断往下移动
heapIfy(arr, 0, heapSize);
// 移动完之后继续将堆顶元素和最后一个元素交换,同时减小heapSize,直到heapSize<=0
swap(arr, 0, --heapSize);
}
}
// 某个数在index位置,能否往上移动
public static void heapInsert(int[] arr, int index) {
// 获取子节点、父节点公式如下:
// 得到左子节点 2*index+1
// 得到右子节点 2*index+2
// 得到父节点 (index-1)/2
// 如果当前的数大于父节点的数则做交换
while (arr[index] > arr[(index - 1) / 2]) {
swap(arr, index, (index - 1) / 2);
index = (index - 1) / 2;
}
}
// 某个数在index位置,能否往下移动
public static void heapIfy(int[] arr, int index, int heapSize) {
// 左子节点的下标
int left = index * 2 + 1;
// 下方还有子节点的时候
while (left < heapSize) {
// 两个子节点中,谁的值大,把下表给largest
int largest = left + 1 < heapSize && arr[left + 1] > arr[left] ? left + 1 : left;
// 父节点和较大的子节点之间,谁的值大,把下标给largest
largest = arr[largest] > arr[index] ? largest : index;
// 如果最大的子节点就是当前节点则跳出循环
if (largest == index) {
break;
}
// 与最大的子节点交换位置
swap(arr, largest, index);
// 更新当前节点的位置
index = largest;
// 更新左子节点的位置
left = index * 2 + 1;
}
}
// 交换数组中的两个元素
public static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
文档信息
- 本文作者:carpe
- 本文链接:https://carpedx.com/wiki/algorithm-heap-sort/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)