归并排序:是创建在归并操作上的一种有效的排序算法。算法是采用分治法的一个非常典型的应用,且各层分治递归可以同时进行。归并排序思路简单,速度仅次于快速排序,为稳定排序算法,一般用于对总体无序,但是各子项相对有序的数列。
基本思想
归并排序是用分治思想,分治模式在每一层递归上有三个步骤:
- 分解(Divide):将n个元素分成个含n/2个元素的子序列。
- 解决(Conquer)*:用合并排序法对两个子序列递归的排序。
- 合并(Combine):合并两个已排序的子序列已得到排序结果。
实现逻辑
递归法
- 将序列每相邻两个数字进行归并操作,形成floor(n/2)个序列,排序后每个序列包含两个元素
- 将上述序列再次归并,形成floor(n/4)个序列,每个序列包含四个元素
- 重复步骤②,直到所有元素排序完毕
迭代法
- 申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列
- 设定两个指针,最初位置分别为两个已经排序序列的起始位置
- 比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置
- 重复步骤③直到某一指针到达序列尾
- 将另一序列剩下的所有元素直接复制到合并序列尾
动图演示
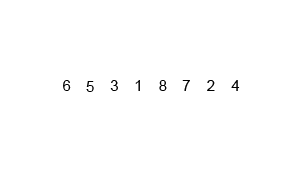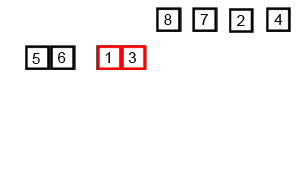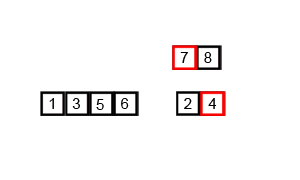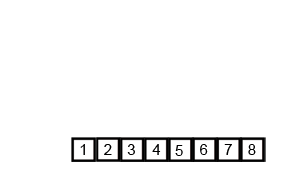
java
相关代码:二分查找算法
public static void main(String[] args) {
// 初始化一个整型数组
int[] arr = {9, 3, 4, 6, 2, 5, 7, 1, 8};
// 调用归并排序函数,对数组进行排序
mergeSort(arr);
// 打印排序后的数组
System.out.println(Arrays.toString(arr));
}
// 归并排序函数,接收一个整型数组作为参数,对其进行排序
public static void mergeSort(int[] arr) {
// 如果数组为空或者只有一个元素,则直接返回,不需要排序
if (arr == null || arr.length < 2) return;
// 调用递归排序函数,传入数组和范围参数,对数组进行递归排序
process(arr, 0, arr.length - 1);
}
// 递归排序函数,接收一个整型数组和两个整数L、R作为参数,表示对数组中[L...R]范围内的元素进行排序
public static void process(int[] arr, int L, int R) {
// 如果范围只有一个元素,则直接返回,不需要排序
if (L == R) return;
// 计算范围的中间点索引,使用位运算加速计算
int mid = L + ((R - L) >> 1); // 中间点索引
// 递归调用process函数,对左半部分[L...mid]进行排序
process(arr, L, mid);
// 递归调用process函数,对右半部分[mid+1...R]进行排序
process(arr, mid + 1, R);
// 调用合并函数,将左右两部分合并为一个有序序列
merge(arr, L, mid, R);
}
// 合并函数,接收一个整型数组和三个整数L、M、R作为参数,表示将数组中[L...M]和[M+1...R]两个有序序列合并为一个有序序列
public static void merge(int[] arr, int L, int M, int R) {
// 创建一个临时数组,用于存储合并后的有序序列
int[] help = new int[R - L + 1];
// 初始化临时数组的索引为0
int i = 0;
// 初始化左半部分的索引为L
int p1 = L;
// 初始化右半部分的索引为M+1
int p2 = M + 1;
// 循环比较左右部分
while (p1 <= M && p2 <= R) {
// 进行排序 如果左半部分当前下标值小,就将值放入临时数组然后下标+1,否则右半部分下标+1
help[i++] = arr[p1] <= arr[p2] ? arr[p1++] : arr[p2++];
}
// 将第一个有序序列中剩余的元素存入临时数组中
while (p1 <= M) {
help[i++] = arr[p1++];
}
// 将第二个有序序列中剩余的元素存入临时数组中
while (p2 <= R) {
help[i++] = arr[p2++];
}
// 将临时数组中的元素复制回原数组中对应的位置,完成合并操作
for (i = 0; i < help.length; i++) {
arr[L + i] = help[i];
}
}
用Master公式分析时间复杂度:
1)用Master公式计算上面归并排序的时间复杂度公式为:T(N)=2*T(N/2)+O(N^1)
根据这个公式可知:a=2,b=2,d=1
2)计算结果(对应公式 log(b,a)=d 时间复杂度为O(N*logN)):
# log(2,2) = 1
log(b,a) = d
# O(N*logN)
O(N*logN) # 结果为 O(N*logN)
所以时间复杂度为:O(N*logN)
文档信息
- 本文作者:carpe
- 本文链接:https://carpedx.com/wiki/algorithm-merge-sort/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)