carpe

algorithm - 快速排序

Wiki algorithm

快速排序，又称分区交换排序，简称快排，是一种被广泛运用的排序算法

基本思想

通过将待排记录分隔成独立的两部分，其中一部分记录比关键字小的，另一部分记录比关键字大的，分别对这两部分记录进行排序，以达到整个序列有序

实现逻辑

快速排序使用分治法策略来把一个序列分为两个子序列

  1. 从数列中挑出一个元素，称为 “基准”（pivot）
  2. 比基准值小的摆放在基准左边，比基准值大的摆在基准右边
  3. 递归把左边和右边的子数排序

复杂度

最佳空间复杂度：O(logN)
最差空间复杂度：O(N)

最佳时间复杂度：O(N*logN)
最差时间复杂度：O(N^2)

动图演示

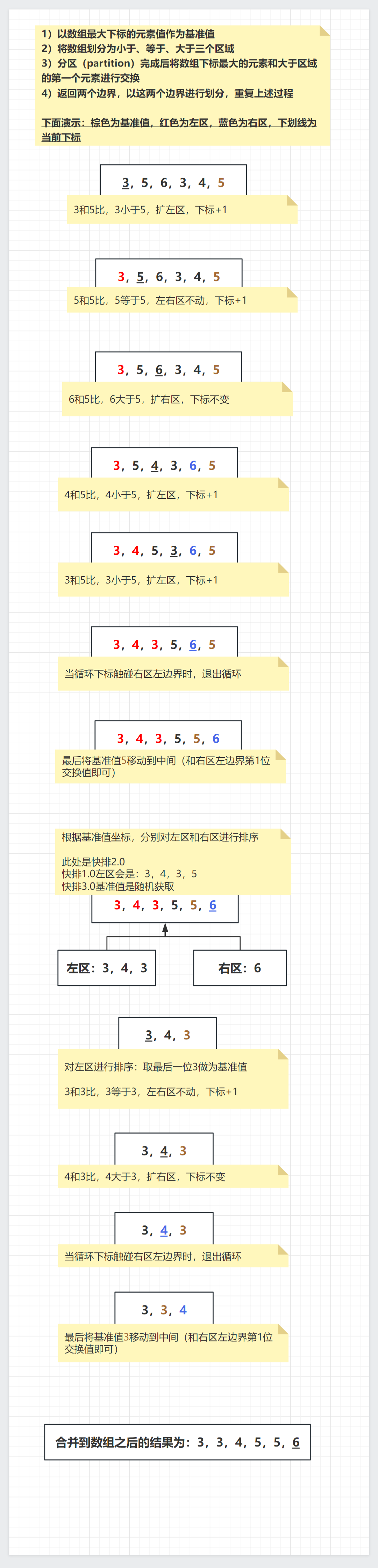
流程图

java

public static void main(String[] args) {
    int[] arr = {3, 5, 6, 3, 4, 5, 2, 6, 9, 0};
    quickSort(arr);
    System.out.println(Arrays.toString(arr));
}

// 快速排序入口函数
public static void quickSort(int[] arr) {
    if (arr == null || arr.length < 2) return;

    quickSort(arr, 0, arr.length - 1);
}

// 快速排序递归函数，对arr[L..R]进行排序
public static void quickSort(int[] arr, int L, int R) {
    if (L >= R) return;

    // 快排3.0 取随机数作为基准值，跟数组最后一位做交换
    // 随机这一下，常数时间比较大
	// 但只有这一下随机，才能在概率上把快速排序的时间复杂度收敛到O(n * logn)
    swap(arr, L + (int) (Math.random() * (R - L + 1)), R);
    int[] p = partition(arr, L, R);
    // 对小于基准值的子数组进行递归排序
    quickSort(arr, L, p[0] - 1);
    // 对大于基准值的子数组进行递归排序
    quickSort(arr, p[1] + 1, R);
}

// 分区函数，处理arr[L..R]的数组，返回等于区域的左右边界
public static int[] partition(int[] arr, int L, int R) {
    // 小于区域的右边界	从-1开始
    int less = L - 1;
    // 大于区域的左边界 从arr.length-1开始
    int more = R;
    while (L < more) {  // 当前数的位置为L，基准值为arr[R]
        if (arr[L] < arr[R]) {  // 当前数小于基准值
            // 将当前数放入小于区域，并将L向右移动
            swap(arr, ++less, L++);
        } else if (arr[L] > arr[R]) {   // 当前数大于基准值
            // 将当前数放入大于区域，并将L向右移动
            swap(arr, --more, L);
        } else {
            // 当前数等于基准值，将L向右移动
            L++;
        }
    }
    // 将基准值放入等于区域的右边界位置
    swap(arr, more, R);
    // 返回等于区域的左右边界
    return new int[] {less + 1, more};
}

// 交换数组中的两个元素的位置
public static void swap(int[] arr, int i, int j) {
    int tmp = arr[i];
    arr[i] = arr[j];
    arr[j] = tmp;
}

文档信息

Search

    Table of Contents